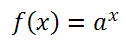środa, 17 grudnia 2014
Zagadka 8
Nasz konkurs niestety dobiega już końca, ale cieszymy się, że poświęciliście czas i rozwiązywaliście zagadki razem z nami. To już ostatnia z nich, a odpowiedzi możecie wysyłać do jutra do godziny 12:00. Rozstrzygnięcie i rozdanie nagród odbędzie się w piątek :)
wtorek, 16 grudnia 2014
Zagadka 7
Dzisiaj ekipa naszego bloga zmierzyła się z próbną maturą z matematyki, miejmy nadzieję, że poszła dobrze :) Tymczasem mamy dla Was przedostatnią już zagadkę. Pamiętajcie, że konkurs trwa do jutra! Jeśli nie wysłaliście nam wszystkich rozwiązań, zróbcie to jak najszybciej. Powodzenia :)
"Wino i sok"
Winicjusz upił z pełnego pucharu wina (o pojemności 2 l) jedną trzecią i dolał soku. Potem wypił pół pucharu i znowu dolał soku. Następnie wypił jedną szóstą i znowu dolał soku. Na koniec wypił cały puchar.
poniedziałek, 15 grudnia 2014
Zagadka 6
"Spacer"
Mąż zawrócił i przyjechali do domu dokładnie w godzinę i 50 minut po jego wyjeździe.
Ile czasu szła pani Jola drogą, zanim spotkała męża?
niedziela, 14 grudnia 2014
Zagadka nr 5
W niedzielny wieczór polecamy trochę gimnastyki umysłu!
Magda, Weronika, Justyna i Domi obchodzą imieniny tego samego dnia. Z tej racji każda z nich kupuje w kwiaciarni "U Ady" 7 tulipanków i obdziela nimi każdą z trzech przyjaciółek. Tak się składa, że każda otrzymuje 7 kwiatków. W rzeczywistości Magda podarowała 5 czerwonych tulipanów Weronice , Weronika dała dwa żółte Magdzie, a Justyna - trzy niebieskie Domi.
Ile tulipanów otrzymała Justyna od Domi?
sobota, 13 grudnia 2014
Zagadka 4
Gotowi na kolejną zagadkę?
Rybak złowił karpia. Na pytanie, jak wielka jest zdobycz, odpowiedział zagadkowo jakby chciał wybadać inteligencję pytającego: "Łeb karpia mierzy 12 cm, tułów ma długość taką jak łeb i ogon razem, przy czym trzy czwarte ogona mierzą tyle ile łeb i czwarta część głowy".
"Karp"
Rybak złowił karpia. Na pytanie, jak wielka jest zdobycz, odpowiedział zagadkowo jakby chciał wybadać inteligencję pytającego: "Łeb karpia mierzy 12 cm, tułów ma długość taką jak łeb i ogon razem, przy czym trzy czwarte ogona mierzą tyle ile łeb i czwarta część głowy".
Jak duży był karp?
Powodzenia! :)
piątek, 12 grudnia 2014
Zagadka nr 3
Cieszymy się, że znaleźli się śmiałkowie, którzy rozwiązują na bieżąco nasze zadania. Jednak mamy nadzieję, że inni zdecydują się przyłączyć do naszej zabawy. Konkurs trwa do środy, więc do dzieła. Czekamy na Wasze maile, a tymczasem nowa łamigłówka. Zaczynamy!
.gif)
Przypuśćmy, że następujące zdania są prawdziwe:
1. Wszyscy Rosjanie są cierpliwi,
2. Pewni Rosjanie są nauczycielami,
3. Pewni nauczyciele nie są cierpliwi,
4. Wszyscy nauczyciele są wykształceni.
Wobec tego, które z następujących zdań muszą być prawdziwe, a które muszą być fałszywe(napiszcie tylko te, o których jesteście pewni!):
5. Cierpliwi Rosjanie są nauczycielami,
6. Cierpliwi nauczyciele są Rosjanami,
7. Rosyjscy nauczyciele są cierpliwi,
8. Pewni nauczyciele nie są Rosjanami,
9. Pewni wykształceni nauczyciele nie są cierpliwi,
10. Cierpliwi nauczyciele nie są wykształceni.
Powodzenia!
czwartek, 11 grudnia 2014
Zagadka 2
Jest nam bardzo miło, że zainteresowaliście się konkursem i wczoraj otrzymaliśmy już kilka wiadomości. Jeżeli ktoś nie rozwiązał naszej wczorajszej zagadki, to nic straconego! Na Wasze e-maile czekamy do przyszłej środy. Tymczasem mamy dla was nowe wyzwanie. Gotowi?
"Przeprawa przez Wołgę"
Oddział liczący wraz z generałem 12 żołnierzy ma się przeprawić przez rzekę. Mostu nie ma, a nurt rzeki jest zbyt wartki, żeby pokonać ją wpław. Generał spostrzega na tym samym brzegu małą łódkę i dwóch stojących przy niej chłopców. Kłopot polega na tym, że łódka jest tak mała, że może pomieścić albo jednego żołnierza, albo dwóch chłopców. Jak przeprawić cały oddział tą małą łódką?
Podaj najmniejszą liczbę kursów, które trzeba wykonać.
Czekamy na Wasze rozwiązania :)
środa, 10 grudnia 2014
Zagadka 1
Postanowiliśmy trochę ożywić naszego bloga i zorganizowaliśmy dla Was konkurs. Od dzisiaj do przyszłej środy będziemy codziennie publikować jedną zagadkę matematyczną. Rozwiązania możecie wysyłać na nasz adres: nieumiemtegozadania@gmail.com w tytule wpisując swoje imię i nazwisko oraz klasę. Dla osób, które rozwiążą największa ilość zagadek przewidziane są ciekawe nagrody. Jeśli zdarzy się, że kilka osób zdobędzie tyle samo punktów, pod uwagę będzie brana kolejność wysyłanych wiadomości. Pamiętajcie też, aby w swoich rozwiązaniach podawać wyjaśnienie. Gorąco zachęcamy do wzięcia udziału w naszym konkursie i życzymy powodzenia! :)
"Za droga piłka"
Dwaj bracia, Szymon i Konrad, wybrali się do sklepu sportowego, aby kupić piłkę do siatkówki. Niestety, żaden z nich nie miał odpowiedniej kwoty. Szymon zorientował się, że brakuje mu 2 złotych, a Konradowi brakowało aż 24 złotych. Kiedy zebrali razem swoje pieniądze, nadal mieli ich za mało, aby kupić piłkę.
Ile kosztowała piłka?
Czekamy na wasze rozwiązania!
sobota, 6 grudnia 2014
Liczba π
Zapewne wielu z Was miało już do czynienia z liczbą π [czyt. pi], a już niemalże każdy słyszał o niej. Ta stała matematyczna wykorzystywana jest w wielu dziedzinach zarówno matematyki jak i fizyki. Geometria eukledisowa przedstawia ją jako stosunek długości obwodu koła do jego średnicy. Jednak definiuje się ją też jako np. pole koła o promieniu równym 1 albo jako najmniejszą dodatnią wartość x, dla której funkcja sinus przyjmuje wartość 0.
Ponadto liczba π jest niewymierna, a to oznacza, że nie możemy jej zapisać w postaci ilorazu dwóch liczb całkowitych oraz jest liczbą przestępną, czyli nie istnieje taki wielomian o współczynnikach całkowitych, którego π jest pierwiastkiem. Co prawda w wielu obliczeniach wykorzystujemy przybliżenia tej liczby, najczęściej przyjmujemy wartość π ≈ 3,14 lub π ≈ 22/7, lecz nie ma tu równości. Często używa się też ułamka 355/113, lecz to nadal nie daje nam pełnego rozwinięcia dziesiętnego. Tak naprawdę posiada ona nieskończenie wiele miejsc po przecinku, więc nie jest możliwe podane jej dokładnej wartości.
Pozdrawiamy i życzymy udanego weekendu!
Matblog ;)
Ponadto liczba π jest niewymierna, a to oznacza, że nie możemy jej zapisać w postaci ilorazu dwóch liczb całkowitych oraz jest liczbą przestępną, czyli nie istnieje taki wielomian o współczynnikach całkowitych, którego π jest pierwiastkiem. Co prawda w wielu obliczeniach wykorzystujemy przybliżenia tej liczby, najczęściej przyjmujemy wartość π ≈ 3,14 lub π ≈ 22/7, lecz nie ma tu równości. Często używa się też ułamka 355/113, lecz to nadal nie daje nam pełnego rozwinięcia dziesiętnego. Tak naprawdę posiada ona nieskończenie wiele miejsc po przecinku, więc nie jest możliwe podane jej dokładnej wartości.
Używany dzisiaj symbol π wprowadzony został dopiero w 1706 roku przez Wiliama Jonesa, a spopularyzował go Leonhard Euler używając tego zapisu w dziele Analiza. Swą nazwę zawdzięcza pierwszej literze greckiego słowa "peryferia". Liczba ta nazywana jest również ludolfiną od imienia niemieckiego matematyka Ludolpha van Ceulena, który wraz z żoną na początku XVII w. podał jej przybliżenie z dokładnością 35 miejsc po przecinku, co w tamtych czasach było ogromnym wyczynem. Liczba π popularność zawdzięcza występowaniu swoim we wzorach na pole koła czy objętości kuli, związana jest także z kwadraturą koła - zadaniem pochodzącym ze starożytnej Grecji, rozwiązanym dopiero przez Lindemanna.
Liczba pi posiada nawet swoich wielbicieli! A do nich zalicza się ekipa naszego bloga :) Światowy Dzień Liczby Pi przypada na 14 marca, wynika to z amerykańskiego sposobu zapisywania dat, najprostsze przybliżenie - "3,14" - wyznacza właśnie tę datę. Ze względu na europejski sposób zapisu dat, tutejszym odpowiednikiem tego święta jest Dzień Aproksymacji Liczby π, który przypada na 22 lipca (ułamek 22/7).
Powstało nawet sporo wierszy, wierszyków i kilka filmów o jej tematyce. Księga Guinnessa zawiera listę ludzi którzy zapamiętali najwięcej cyfr liczby Pi.
Jak wcześniej wspomnieliśmy, również należymy do grona jej miłośników. Udowadniając to, już dwa lata z rzędu zorganizowaliśmy szkolne obchody Dnia Liczby Pi. Konkursy, zagadki i π-przekąski zainteresowały naszych rówieśników, o czym możecie poczytać m. in. tu:
http://sieradz.com.pl/wiadomosci/sieradz/2275,dzien-liczby-pi-w-jagiellonczyku.html
lub tu:
http://sieradz.naszemiasto.pl/artykul/dzien-liczby-pi-w-i-lo-w-sieradzu-zdjecia,2197028,artgal,t,id,tm.html
http://sieradz.com.pl/wiadomosci/sieradz/2275,dzien-liczby-pi-w-jagiellonczyku.html
lub tu:
http://sieradz.naszemiasto.pl/artykul/dzien-liczby-pi-w-i-lo-w-sieradzu-zdjecia,2197028,artgal,t,id,tm.html
Pozdrawiamy i życzymy udanego weekendu!
Matblog ;)
niedziela, 23 listopada 2014
Mat-Wykłady!
W miniony piątek poprowadziliśmy dwa 45-minutowe wykłady dla młodszych klas z naszej szkoły. Tematem prezentacji były, wspomniane już na naszym blogu, grafy i matematyka w życiu. Ponadto, chcąc zachęcić i "rozbudzić" słuchających przygotowaliśmy kilka zagadek i zadań logicznych. O ile w czasie pierwszego spotkania czuliśmy się nieco niepewnie, to następny wykład udało się zorganizować precyzyjniej :)
Obawialiśmy się, że młodsi koledzy i koleżanki mogą nie zainteresować się tematem, jednak, na szczęście, nic takiego nie miało miejsca. Atmosfera sprzyjała, by zajęcia trwały dokładnie całą godzinę lekcyjną. By podziękować wszystkim za uwagę, przygotowaliśmy także słodkie upominki w postaci cukierków dla każdego z uczniów.
Musimy przyznać, że spodobała nam się taka forma propagowania matematyki i jeśli tylko nadarzy się kolejna okazja do zorganizowania takiego spotkania, na pewno z niej skorzystamy! :)
Poniżej wstawiamy kilka zdjęć z wykładów.
Pozdrawiamy,
Mat-Blog!
.JPG)
Obawialiśmy się, że młodsi koledzy i koleżanki mogą nie zainteresować się tematem, jednak, na szczęście, nic takiego nie miało miejsca. Atmosfera sprzyjała, by zajęcia trwały dokładnie całą godzinę lekcyjną. By podziękować wszystkim za uwagę, przygotowaliśmy także słodkie upominki w postaci cukierków dla każdego z uczniów.
Musimy przyznać, że spodobała nam się taka forma propagowania matematyki i jeśli tylko nadarzy się kolejna okazja do zorganizowania takiego spotkania, na pewno z niej skorzystamy! :)
Poniżej wstawiamy kilka zdjęć z wykładów.
Pozdrawiamy,
Mat-Blog!
wtorek, 18 listopada 2014
"Stary, Polak potrafi, uwierz!"
Słyszeliście dużo o perskich
dywanach i wiecie z pewnością, że w każdym samochodzie musi być
ostrzegawczy trójkąt. Lubicie tęz patrzeć na księżyc i szukać
kraterów. A niejeden z Was chciałby bedąc w Chinach nakleić
znaczek i wysłac go do Polski. Co to ma wspólnego z matmą? Otóż
właśnie z Polski pochodzą niemalże równie sławne dywany i
trójkąty Sierpińskiego, a jeden z kraterów na srebrnym globie
nosi właśnie jego imię. Natomiast w Państwie Środka Chińczyków
budzą listy ze znaczkami, na których widnieje polski akcent. Ale od początku.
Wacław Sierpiński to jeden z najbardziej wybitnych
matematyków Ip. XX w. Zajmowała go mnogość i teoria liczb. Jednak
z „przyziemną” matematyką nie radził sobie prawie w ogóle.
Gdy żona powierzyła mu budżet domowy, gubił się w rachunkach i
papierach. Żona ponoć powiedziała do niego : „Ty się do matematyki zupełnie nie nadajesz”. W tym samym roku odebrał on profesurę nadzwyczajną na Uniwersytecie Lwowskim.
Jego działalność można podzielić na kilka okresów. Pierwszy z nich to ten poświęcony toerii liczb. Jest to skomplikowane zagadnienie i nie będziemy go tutaj rozwijać, jednak był to krok milowy w teorii ekwipatrycji(o której więcej tutaj), a także w całej matematyce, gdy jego dowody i teorie zaczęły podważać uważane dotąd za aksjomaty niewymagające dowodów.
Następny jego etap jest nam bardziej znany, ponieważ dotyczy bliższych nam zagadnień.
Mając trójkąt równoboczny, dzielimy go na 4 przystające. Wyrzucamy środkowy i powtarzamy tę operację na każdym następnym. W efekcie, w granicy otrzymamy krzywą, zwaną trójkątem Sierpińskiego. Podobnie dzieląc kwadrat na 9 części, wyrzucając środkowy, dojdziemy do tkw. „dywanu Sierpińskiego” .Są to przykłady fraktali, których badanie zaczęło się właśnie od tych przykładów.
Barwny życiorys polskiego matematyka, ponad
700 wydanych prac i 50 napisanych książek stały się powodem, aby
nazwać jeden z kraterów na księżycu właśnie jego imieniem.
Możemy być dumni, że nie czytamy o żadnym zagranicznym, ale o
polskim profesorze.
Mamy nadzieję, że choć trochę
zachęciliśmy Was do zainteresowania się Królową Nauk. Kto wie,
może ktoś z czytających ten artykuł będzie widniał za
kilkanaście lat na chińskich znaczkach, upamiętniających
kolejnych wielkich matematyków? ;)
Pozdrwiamy,
MatBlog
Pozdrwiamy,
MatBlog
niedziela, 9 listopada 2014
Sinus,cosinus,tangens,cotangens... Skąd to się wzięło?
Zapewne nieraz gdy stosowaliście w swych obliczeniach funkcje trygonometryczne zastanawialiście się, w jaki sposób one powstały. Wielu z was nurtowało też pewnie pytanie, skąd wzięły się nazwy tych funkcji i kto je stworzył. Dzisiaj postaramy się odpowiedzieć na te pytania. Zatem zaczynamy :)
Co to jest trygonometria?
Trygonometria jest działem matematyki, którego przedmiotem badań są związki miarowe między bokami i kątami trójkątów oraz funkcje trygonometryczne. Trygonometria powstała i rozwinęła się głównie w związku z zagadnieniami pomiarów na powierzchni Ziemi oraz potrzebami żeglugi morskiej (określenia położenia i kierunku przy pomocy ciał niebieskich). Na rozwój trygonometrii miały też znaczący wpływ badania astronomiczne.
Skąd wzięły się nazwy funkcji trygonometrycznych?
Nazwy funkcji trygonometrycznych, którymi się obecnie posługujemy pochodzą z języka łacińskiego. Nazwy te powstawały w bardzo różny sposób, warto więc przyjrzeć się ich etymologiom:
Historia trygonometrii.
Twierdzenia dotyczące stosunków boków trójkątów podobnych znano już w starożytnym Egipcie i Babilonie, jednak społeczeństwa te nie znały idei miary kąta i badały tylko własności boków. Dopiero w starożytnej Grecji powstały twierdzenia będące protoplastami dzisiejszej trygonometrii. Zawarto je w formie geometrycznej w dziełach Euklidesa i Archimedesa. Na przykład propozycje XII i XIII z Księgi II Elementów są tożsame ze wzorem cosinusów odpowiednio dla kątów rozwartych i ostrych. Twierdzenia dotyczące długości cięciw są natomiast zastosowaniem wzoru sinusów. Jedno z twierdzeń Archimedesa jest zaś odpowiednikiem wzoru na sinus sumy i różnicy kątów. Matematycy za czasów Arystarcha z Samos dla celów obliczeniowych używali m.in. twierdzenia mówiącego, iż:
Pierwsze tablice trygonometryczne zostały prawdopodobnie skompilowane przez Hipparcha (180-125 p.n.e.). Hipparch jako pierwszy ułożył tablice odpowiadających sobie długości cięciwy i łuku dla różnych kątów. Dzięki tablicy Hipparcha spopularyzowany został podział kąta pełnego na 360 stopni, który jest stosowany do dziś.
W X wieku islamscy matematycy używali wszystkich sześciu funkcji trygonometrycznych z secansem i cosecansem włącznie, co wiadomo dzięki pracy autorstwa Abu al-Wafa. Abu al-Wafa stworzył tablice sinusa z krokiem 0,25° i dokładnością 8 cyfr dziesiętnych a także dokładne tablice tangensa. Zauważył również tożsamość, która jest używana do dziś:
Traktaty dotyczące trygonometrii zaprezentowali Bhāskara Acārya i Nasir ad-Din Tusi w XIII wieku. Drugi z nich sformułował i udowodnił twierdzenie sinusów, sklasyfikował też sześć różnych przypadków prostokątnych trójkątów sferycznych.
W XIV wieku Ghiyath al-Kashi stworzył tablice sinusa z dokładnością do czterech cyfr sześćdziesiątkowych (odpowiednik 8 miejsc dziesiętnych) dla każdego stopnia. Uług Beg (XV wiek) także podał dokładne tablice sinusa i tangensa sięgające 8 miejsc
W dziedzinie trygonometrii Europejczycy byli przez długi czas daleko w tyle za Hindusami, Arabami i Persami. Dopiero w epoce renesansu europejscy matematycy zaczęli wprowadzać funkcje trygonometryczne. Jednym z nich był wybitny polski astronom i matematyk Mikołaj Kopernik, który w swym słynnym dziele ,,O obrotach sfer niebieskich” z 1543r. zawarł nie tylko teorię heliocentryczną, ale też m.in. pojęcie funkcji secans, która dotychczas nie była znana w Europie.
Co to jest trygonometria?
Trygonometria jest działem matematyki, którego przedmiotem badań są związki miarowe między bokami i kątami trójkątów oraz funkcje trygonometryczne. Trygonometria powstała i rozwinęła się głównie w związku z zagadnieniami pomiarów na powierzchni Ziemi oraz potrzebami żeglugi morskiej (określenia położenia i kierunku przy pomocy ciał niebieskich). Na rozwój trygonometrii miały też znaczący wpływ badania astronomiczne.
Skąd wzięły się nazwy funkcji trygonometrycznych?
Nazwy funkcji trygonometrycznych, którymi się obecnie posługujemy pochodzą z języka łacińskiego. Nazwy te powstawały w bardzo różny sposób, warto więc przyjrzeć się ich etymologiom:
- Sinus był w pracach hinduskiego matematyka Aryabhaty w sanskrycie nazywany ,,ardha-jiva" ("połowa cięciwy"), co zostało skrócone do ,,jiva", a następnie transliterowane do arabskiego ,,jiba". Europejscy tłumacze, Robert z Chester i Gerardo z Cremony w XII-wiecznym Toledo pomylili ,,jiba" z ,,jaib" , oznaczającym "zatokę" prawdopodobnie dlatego, że ,,jiba" i ,,jaib" są tak samo pisane po arabsku (informacja o samogłoskach jest gubiona w piśmie). Sinus znaczy po łacinie właśnie zatoka.
- Tangens pochodzi od łacińskiego tangere – dotykający, styczny.
- Secans pochodzi z łacińskiego secare – dzielić, rozcinać, rozstrzygać i znaczy odcięcie.
- Cosinus, cotangens i cosecans powstały przez złożenie łacińskiego co- (wspólnik, towarzysz) i słów sinus, tangens i secans. Pierwotnie cosinus był nazywany complementi sinus, czyli sinus kąta dopełniającego. Rzeczywiście jest on równy sinusowi miary kąta dopełniającego. Podobnie cotangens i cosecans są równe tangensowi i secansowi tego kąta. Przedrostek "ko-" był jednak używany w stosunku do cosinusa już w sanskrycie u Aryabhaty (koti-jya, kojya); trudno określić, w jakim stopniu nazwa łacińska do tego nawiązuje.
Historia trygonometrii.
Twierdzenia dotyczące stosunków boków trójkątów podobnych znano już w starożytnym Egipcie i Babilonie, jednak społeczeństwa te nie znały idei miary kąta i badały tylko własności boków. Dopiero w starożytnej Grecji powstały twierdzenia będące protoplastami dzisiejszej trygonometrii. Zawarto je w formie geometrycznej w dziełach Euklidesa i Archimedesa. Na przykład propozycje XII i XIII z Księgi II Elementów są tożsame ze wzorem cosinusów odpowiednio dla kątów rozwartych i ostrych. Twierdzenia dotyczące długości cięciw są natomiast zastosowaniem wzoru sinusów. Jedno z twierdzeń Archimedesa jest zaś odpowiednikiem wzoru na sinus sumy i różnicy kątów. Matematycy za czasów Arystarcha z Samos dla celów obliczeniowych używali m.in. twierdzenia mówiącego, iż:
sinα/sinβ<α/β<tgα/tgβ dla 0°<β<α<90°
Pierwsze tablice trygonometryczne zostały prawdopodobnie skompilowane przez Hipparcha (180-125 p.n.e.). Hipparch jako pierwszy ułożył tablice odpowiadających sobie długości cięciwy i łuku dla różnych kątów. Dzięki tablicy Hipparcha spopularyzowany został podział kąta pełnego na 360 stopni, który jest stosowany do dziś.
Hipparchos z Nikei (Hipparch)
Później Klaudiusz Ptolemeusz (ok. 90 - ok. 168 n.e.) rozbudował w swoim dziele ,,Almagest" koncepcję "cięciw na okręgu" Hipparcha. Trzynasta księga ,,Almagestu" była znaczącą starożytną pracą w dziedzinie trygonometrii. Jedno z jej twierdzeń jest dziś znane jako twierdzenie Ptolemeusza. Szczególny przypadek twierdzenia Ptolemeusza pojawia się także w Propozycji XCIII dzieła Euklidesa. Twierdzenie Ptolemeusza prowadzi do równoważnika wzorów na sinus i cosinus sumy i różnicy, choć oczywiście wyrażonych w języku cięciw, a nie funkcji. Ptolemeusz wyprowadził później ekwiwalent wzoru:
Na podstawie swoich twierdzeń Ptolemeusz stworzył później własne tablice trygonometryczne, które podobnie jak tablice Hipparcha nie przetrwały do czasów współczesnych, jednak dzięki wzmiankom u innych autorów nie ma wątpliwości, że istniały.
Klaudiusz Ptolemeusz
Wielki wkład w rozwój trygonometrii mieli także Hindusi. Indyjski matematyk i astronom Aryabhata (476–550 n.e.) w swoim dziele ,,Aryabhata-Siddhanta” po raz pierwszy zdefiniował sinus w znanej po dziś dzień formie, a także cosinus, sinus versus i arcus sinus. Jego dzieła zawierają najwcześniejsze tablice trygonometryczne, które przetrwały do dzisiaj, z wartościami funkcji sinus i sinus versus co 3.75° stopnia od 0° do 90°, z dokładnością do czterech miejsc znaczących.
Aryabhata
Inni hinduscy matematycy rozwinęli później pracę Aryabhaty. Jednym z nich był Varahamihira, który już w VI wieku n.e. używał wzorów, z których korzystamy do dzisiaj choćby na lekcjach matematyki. Są to m.in. wzory redukcyjne oraz tzw. jedynka trygonometryczna.
W VII wieku Bhaskara I stworzył wzór pozwalający na przybliżone obliczanie sinusa dla kąta ostrego bez tablic (z błędem mniejszym od 1,9%):
W VII wieku Bhaskara I stworzył wzór pozwalający na przybliżone obliczanie sinusa dla kąta ostrego bez tablic (z błędem mniejszym od 1,9%):
W końcu VII wieku, Brahmagupta na podstawie wzorów Varahamihiry wyprowadził następujący wzór:
Brahmagupta stworzył także wzór interpolacyjny Brahmagupty, który umożliwił mu stablicowanie wartości sinusa.
Osiągnięcia Hindusów zostały później przetłumaczone, przejęte i rozszerzone przez arabskich i perskich matematyków. Jednym z nich był Muhammad ibn Musa al-Chuwarizmi, który w IX wieku obliczył dokładne tablice sinusa i cosinusa i pierwsze w historii tablice tangensa.W X wieku islamscy matematycy używali wszystkich sześciu funkcji trygonometrycznych z secansem i cosecansem włącznie, co wiadomo dzięki pracy autorstwa Abu al-Wafa. Abu al-Wafa stworzył tablice sinusa z krokiem 0,25° i dokładnością 8 cyfr dziesiętnych a także dokładne tablice tangensa. Zauważył również tożsamość, która jest używana do dziś:
sin2x=2cosxsinx
Traktaty dotyczące trygonometrii zaprezentowali Bhāskara Acārya i Nasir ad-Din Tusi w XIII wieku. Drugi z nich sformułował i udowodnił twierdzenie sinusów, sklasyfikował też sześć różnych przypadków prostokątnych trójkątów sferycznych.
W XIV wieku Ghiyath al-Kashi stworzył tablice sinusa z dokładnością do czterech cyfr sześćdziesiątkowych (odpowiednik 8 miejsc dziesiętnych) dla każdego stopnia. Uług Beg (XV wiek) także podał dokładne tablice sinusa i tangensa sięgające 8 miejsc
W dziedzinie trygonometrii Europejczycy byli przez długi czas daleko w tyle za Hindusami, Arabami i Persami. Dopiero w epoce renesansu europejscy matematycy zaczęli wprowadzać funkcje trygonometryczne. Jednym z nich był wybitny polski astronom i matematyk Mikołaj Kopernik, który w swym słynnym dziele ,,O obrotach sfer niebieskich” z 1543r. zawarł nie tylko teorię heliocentryczną, ale też m.in. pojęcie funkcji secans, która dotychczas nie była znana w Europie.
Pierwsza strona dzieła ,,O obrotach sfer niebieskich" Mikołaja Kopernika
Oprócz Kopernika funkcje trygonometryczne do europejskiej matematyki wprowadzali m.in.: Francesco Maurolico, Edmund Gunter i François Viète.
W 1595 Bartłomiej Pitiscus użył po raz pierwszy terminu "trygonometria" w swoim dziele ,,Trigonometria: sive de solutione triangulorum Tractatus brevis et perspicuus”.
,,Opus palatinum de triangulis” autorstwa Retyka, było prawdopodobnie pierwszą definicją funkcji trygonometrycznych w terminach trójkątów prostokątnych zamiast okręgów jednostkowych; ta praca została dokończona przez Valentina Otho, studenta Rheticusa w roku 1596.
Isaac Newton w 1665 znalazł rozwinięcie funkcji sinus i cosinus w szereg, a Leonhard Euler w 1734 rozwinięcie funkcji sinus w iloczyn nieskończony.
W XVII wieku Isaac Newton i James Stirling stworzyli wzór interpolacyjny Newtona-Stirlinga dla funkcji trygonometrycznych.
,,Opus palatinum de triangulis” autorstwa Retyka, było prawdopodobnie pierwszą definicją funkcji trygonometrycznych w terminach trójkątów prostokątnych zamiast okręgów jednostkowych; ta praca została dokończona przez Valentina Otho, studenta Rheticusa w roku 1596.
Isaac Newton w 1665 znalazł rozwinięcie funkcji sinus i cosinus w szereg, a Leonhard Euler w 1734 rozwinięcie funkcji sinus w iloczyn nieskończony.
W XVII wieku Isaac Newton i James Stirling stworzyli wzór interpolacyjny Newtona-Stirlinga dla funkcji trygonometrycznych.
Jak widać, historia funkcji trygonometrycznych jest niezwykle zawiła. Warto ją jednak poznać, aby wiedzieć, jak powstały prawa i wzory, z których korzystamy obecnie na lekcjach matematyki. Mamy nadzieję, że dzięki naszemu artykułowi trygonometria nie będzie już dla was czymś obcym, a co za tym idzie, stosowanie jej w obliczeniach stanie się łatwiejsze :)
Pozdrawiamy,
Pozdrawiamy,
MatBlog
piątek, 7 listopada 2014
Maturalne powtórki: Przekształcenia wykresu funkcji.
Nareszcie nadszedł wyczekiwany długi weekend, czas upragnionego odpoczynku po tygodniach pełnych sprawdzianów i kartkówek. Każdy potrzebuje czasem chwili dla siebie i błogiego lenistwa, ale nie zapominajcie odwiedzać naszego bloga. Niedawno w skrzynce Pogotowia Matematycznego pojawiły się pierwsze zadania, z czego ogromnie się cieszymy i zachęcamy do dalszego korzystania, gdy tylko natkniecie się na jakikolwiek problem natury matematycznej. W końcu na nas zawsze możecie liczyć! :)
Wracając do powtórek maturalnych, dzisiaj przygotowaliśmy dla Was przekształcenia wykresów funkcji.
Do rysowania wykresów użyłam programu GeoGebra, który z pewnością mogę Wam polecić, gdyż jest łatwy w obsłudze i bardzo intuicyjny.
.bmp)
.bmp)
.bmp)
.bmp)
.bmp)
.bmp)
.bmp)
Wracając do powtórek maturalnych, dzisiaj przygotowaliśmy dla Was przekształcenia wykresów funkcji.
Do rysowania wykresów użyłam programu GeoGebra, który z pewnością mogę Wam polecić, gdyż jest łatwy w obsłudze i bardzo intuicyjny.
Symetria osiowa względem osi OX.
g(x)= - f(x)
Symetria osiowa względem osi OY.
g(x)=f(-x)
Symetria względem początku układu współrzędnych (0,0).
g(x)= -f(-x)
Symetria środkowa względem osi OX.
g(x)=|f(x)|
Symetria środkowa względem osi OY.
g(x)= f(|x|)
Przesunięcie równoległe (translacja) o wektor u=[p,q]
g(x)= f(x-p)+q
Powinowactwo prostokątne o osi OX i skali k.
g(x)=k*f(x)
Powinowactwo prostokątne o osi OY i skali k.
g(x)= f(x/k), k≠0
piątek, 31 października 2014
Zagadka Einsteina
Na zakończenie tygodnia mamy dla Was zagadkę, której autorstwo przypisuje się Albertowi Einsteinowi. Zapraszamy do zapoznania się z jej treścią:
5 ludzi różnych narodowości zamieszkuje 5 domów w 5 różnych kolorach. Wszyscy palą papierosy 5 różnych marek i piją 5 różnych napojów. Hodują zwierzęta 5 różnych gatunków. Który z nich hoduje rybki?
Norweg zamieszkuje pierwszy dom
Anglik mieszka w czerwonym domu.
Zielony dom znajduje się bezpośrednio po lewej stronie domu białego.
Duńczyk pija herbatkę.
Palacz papierosów light mieszka obok hodowcy kotów.
Mieszkaniec żółtego domu pali cygara.
Niemiec pali fajkę.
Mieszkaniec środkowego domu pija mleko.
Palacz papierosów light ma sąsiada, który pija wodę.
Palacz papierosów bez filtra hoduje ptaki.
Szwed hoduje psy.
Norweg mieszka obok niebieskiego domu.
Hodowca koni mieszka obok żółtego domu.
Palacz mentolowych pija piwo.
W zielonym domu pija się kawę.
Zakłada się, że domy ustawione są w jednej linii (1-2-3-4-5), a określenie "po lewej stronie" w punkcie 3. dotyczy lewej strony z perspektywy naprzeciw tych domów (tj. dom o numerze n jest bezpośrednio po lewej stronie domu n+1).
Powodzenia w "główkowaniu"! :D
5 ludzi różnych narodowości zamieszkuje 5 domów w 5 różnych kolorach. Wszyscy palą papierosy 5 różnych marek i piją 5 różnych napojów. Hodują zwierzęta 5 różnych gatunków. Który z nich hoduje rybki?
Norweg zamieszkuje pierwszy dom
Anglik mieszka w czerwonym domu.
Zielony dom znajduje się bezpośrednio po lewej stronie domu białego.
Duńczyk pija herbatkę.
Palacz papierosów light mieszka obok hodowcy kotów.
Mieszkaniec żółtego domu pali cygara.
Niemiec pali fajkę.
Mieszkaniec środkowego domu pija mleko.
Palacz papierosów light ma sąsiada, który pija wodę.
Palacz papierosów bez filtra hoduje ptaki.
Szwed hoduje psy.
Norweg mieszka obok niebieskiego domu.
Hodowca koni mieszka obok żółtego domu.
Palacz mentolowych pija piwo.
W zielonym domu pija się kawę.
Zakłada się, że domy ustawione są w jednej linii (1-2-3-4-5), a określenie "po lewej stronie" w punkcie 3. dotyczy lewej strony z perspektywy naprzeciw tych domów (tj. dom o numerze n jest bezpośrednio po lewej stronie domu n+1).
Powodzenia w "główkowaniu"! :D
wtorek, 21 października 2014
Maturalne powtórki: Działania na potęgach i funkcja wykładnicza.
Chociaż pogoda nie zachęca do jakiejkolwiek pracy, a cały dzień najchętniej spędzilibyśmy pod ciepłym kocem z kubkiem kakao, to może warto zerknąć na kolejną powtórkę maturalną. Dzisiaj przygotowaliśmy dla Was wiadomości o funkcji wykładniczej.
Przydatne wzory:
 |
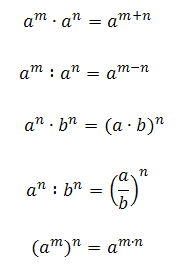| a,b ∈ℝ+ ∧ x,y ∈ℝ |
Funkcja wykładnicza to funkcja określona wzorem
, x∈ℝ ⋀ a>0- D=ℝ ; ZW=(0,∞) ; brak miejsc zerowych
- jeśli a∈(0,1), to funkcja jest malejąca
- jeśli a=1, to funkcja jest stała
- jeśli a∈(0,∞), to funkcja jest rosnąca
- wykres każdej funkcji wykładniczej przechodzi przez punkt (0,1)
.bmp){kind=small}
Nierówności wykładnicze:
Zadania:
1.
2.
3.
4.
Odpowiedzi:
1.
2.
3.
4.
5.
6.
7.
Subskrybuj:
Posty (Atom)